Mundell-Fleming Model

Central Equations of the Mundell-Fleming Model

IS curve: $Y=C(Y-T)+I(r)+G+NX(\epsilon,Y,Y^*)$

LM curve: ${M \over P}=L(r+\pi^e,Y)$

BP curve: $RG=CF(r-r^*)+NX(\epsilon,Y,Y^*)$

where:

$Y\equiv \;$ output

$C\equiv \;$ consumption

$T\equiv \;$ taxes

$I\equiv \;$ investment

$r\equiv \;$ domestic real interest rate

$G\equiv \;$ government spending

$NX\equiv \;$ net exports

$\epsilon\equiv \;$ real exchange rate (foreign currency in terms of domestic currency)

$Y^*\equiv \;$ foreign output

$M\equiv \;$ money supply

$P\equiv \;$ price level

$L\equiv \;$ money demand

$\pi^e\equiv \;$ expected inflation

$RG\equiv \;$ reserve gain (should be zero in equilibrium)

$CF\equiv \;$ capital flows

$r^*\equiv \;$ foreign real interest rate

When totally differentiating the model equations, the following relationships are assumed to hold: ${dC \over d(Y-T)}\equiv \;C_{Y-T}>0$

${dI \over dr}\equiv \;I_r<0$

${dNX \over d\epsilon}\equiv \;NX_\epsilon>0$

${dNX \over dY}\equiv \;NX_Y<0$

${dNX \over dY^*}\equiv \;NX_{Y^*}>0$

${dL \over d(r+\pi^e)}\equiv \;L_{r+\pi^e}<0$

${dL \over dY}\equiv \;L_Y>0$

${dCF \over d(r-r*)}\equiv \;CF_{r-r^*}>0$

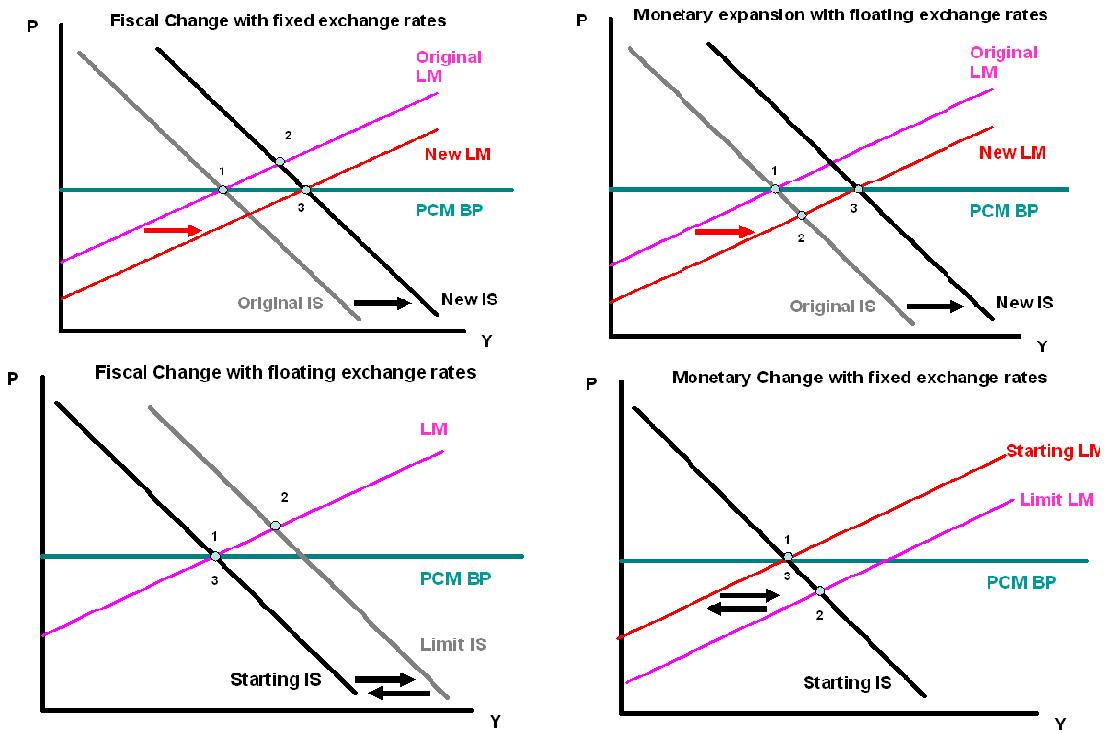
Graphs

Sources

Lectures by Paul Pieper (University of Illinois at Chicago), fall 2004.

David Romer, Advanced Macroeconomics